Через середины двух сторон основания правильной треугольной призмы под углом 30° к...

0 голосов
85 просмотров

Через середины двух сторон основания правильной треугольной призмы под углом 30° к основанию проведена плоскость, пересекающая два боковых ребра. Найдите площадь сечения, если сторона равна 15,7 см.

Прошу помощи! У меня получается ответ ≈ 123 см². В ответах учебника ответ ≈ 92,4 см².

Геометрия | 85 просмотров
0

Интересно, сторона чего равна 15,7 см? Или все ребра равны 15,7 см. ?

оставил комментарий
0

Сторона основания равна 15,7 см?

оставил комментарий
0

Но, вообще-то у правильной призмы все рёбра равны

оставил комментарий
0

Скажите, если у Вас получилось эту задачу решить, ответ. Потому что мне всё-таки кажется, что правильный ответ ≈ 123 см².

оставил комментарий
0

Нет, в прямой правильной призме все рёбра равны отдельно, стороны основания - отдельно. Или все рёбра равны, включая стороны. Но в этой задаче хватает только известной стороны основания 15,7 см.

оставил комментарий
0

ОТВЕТ: 92,43375

оставил комментарий
0

:(Почему у меня не так?..

оставил комментарий
0

Приведу простое решение позже.

оставил комментарий
Дано ответов: 2
0 голосов
Правильный ответ

в сечении получится трапеция... (сорри за грязь на рисунке...)    ее высота-гипотенуза треугольника с углом в 30°; основания =15.7 и 15.7/2 (средняя линия треугольника в основании)    если остались вопросы-с удовольствием отвечу)

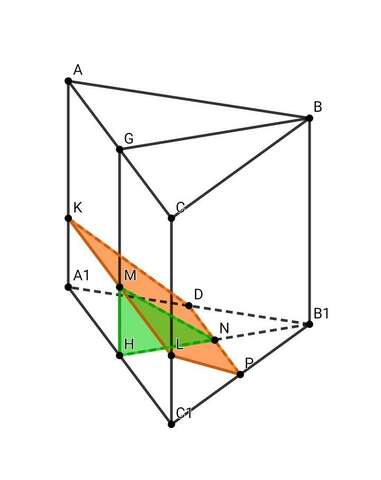
image
0

правильная треугольная призма-это прямая призма с правильным треугольником в основании; высота у нее может быть любая...

оставил комментарий
0 голосов

_____________________________

• В основаниях правильной треугольной призмы лежат правильные треугольники ( тр. АВС = тр. А1В1С1 - равносторонние ). У прямой призмы рёбра равны, перпендикулярны основаниям, параллельны друг другу.

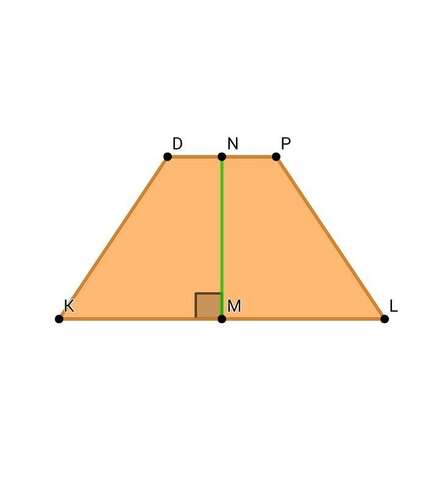
• В сечении правильной треугольной призмы находится равнобедренная трапеция ( DP || KL , KD = LP ).
• DP - средняя линия тр. А1В1С1
DP = ( 1/2 ) • A1C1 = ( 1/2 ) • 15,7 = 15,7 / 2 см.
KL = A1C1 = 15,7 см

• Проведём в тр. А1В1С1 высоту В1Н на А1С1.
В1Н = А1С1•\/3 / 2 = ( 15,7 • \/3 ) / 2 см
НN = ( 1/2 ) • B1H = ( 15,7 • \/3 ) / 4 см

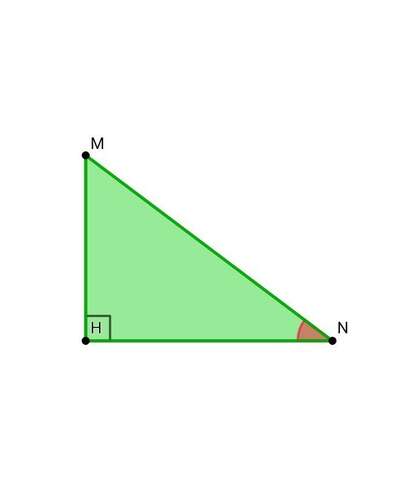
• Рассмотрим тр. МНN (угол МНN = 90°):
cos MNH = HN / MN
cos 30° = ( 15,7 • \/3 ) / 4 : MN

MN = 15,7 / 2 см

• Площадь трапеции KDPL равна:

S = ( 1/2 ) • ( DP + KL ) • MN = ( 1/2 ) • ( 15,7 / 2 + 15,7 ) • 15,7 / 2 = ( 47,1 • 15,7 ) / 8 = 92,43375 см^2

ОТВЕТ: 92,43375 см^2

__________________________

image
image
image
Похожие задачи